ICM的理論突破

Tombos21
7月23日
讀畢需時 7 分鐘

今天，我們將分享自獨立籌碼模型（Independent Chip Model, ICM）發明以來，錦標賽撲克中最重大的理論突破之一。我們開發了一種強大的新技術，使錦標賽玩家能夠以傳統方法所需時間的極小部分解決ICM場景（ICM spots），同時精確度高出數個數量級。通過將這項新技術與GTO Wizard AI整合，多桌錦標賽（MTT）玩家現在可以在幾秒內解決翻牌後ICM場景，即使場上仍有數千名玩家！

ICM：快速回顧

在撲克錦標賽中，籌碼的價值並非恆定。不像現金遊戲中籌碼具有固定價值，在錦標賽中，您的籌碼僅作為生存的手段，試圖在獎金圈中取得尽可能高的排名。這導致了兩個目標之間的錯位：積累籌碼（Chip EV Strategies）與贏得獎金（ICM Strategies）。這就是為什麼創建了獨立籌碼模型（ICM）。

獨立籌碼模型是一種數學公式，以玩家的籌碼量為輸入，輸出每個籌碼量在每個名次的概率。這些名次概率與獎金結構一起，用於計算每個籌碼量的貨幣價值，並可用於優化錦標賽決策。本文解釋了基本ICM公式的運作方式。

翻牌後ICM與籌碼期望值基準

首先值得問的是，積累籌碼與贏得獎金這兩個目標的錯位程度有多大？在之前的文章中，我們對一系列翻牌前推/棄（preflop push/fold）錦標賽進行了籌碼期望值（Chip EV）與ICM策略的基準測試，發現ICM策略顯著優於籌碼期望值。然而，這些實驗僅測試了翻牌前。現在我們有了翻牌後ICM求解（postflop ICM solving），自然的第一步是對翻牌後籌碼期望值與ICM玩家的表現進行基準測試。

設置

1000人參賽的多桌錦標賽（MTT）
100美元買入
15%的玩家進入獎金圈
對稱20大盲（20bb）籌碼

三名競爭者：

籌碼期望值（Chip EV） – 採用固定的納什均衡籌碼期望值策略（Nash Equilibrium Chip EV Strategy）。
GTO Wizard ICM – 採用GTO Wizard AI計算的固定納什均衡ICM策略（Nash Equilibrium ICM strategy）。
Nemesis ICM – 用於基準測試上述兩種策略，Nemesis是一個最大化剝削的表格ICM算法（maximally exploitative tabular ICM algorithm），使用純粹反事實遺憾最小化（pure CFR，無抽象、AI或捷徑），並解決到0.05%底池的極高精確度。

兩場對決

對於每一場對決，我們解決了由籌碼期望值和GTO Wizard ICM計算的納什均衡翻牌策略（Nash Equilibrium flop strategy），然後將其鎖定到Nemesis求解器（nodelocked into the Nemesis solver）中，並測量期望值損失（EV loss）。

籌碼期望值對Nemesis ICM – 首先，我們測量了在翻牌採用博弈論最優（GTO）籌碼期望值策略對抗完美剝削性ICM策略（perfectly exploitative ICM strategy）時的期望值損失。
GTO Wizard ICM對Nemesis ICM – 接下來，我們希望基準測試我們新開發的翻牌後ICM算法的表現。因此，我們讓它對抗Nemesis ICM。請記住，GTO Wizard AI在幾秒內預測最優策略，而Nemesis需要更長的時間。

結果

最直觀的指標是查看這些策略對Nemesis ICM損失了多少金錢。您可以按翻牌前行動過濾此圖表，並查看ICM在哪些錦標賽階段變得重要：

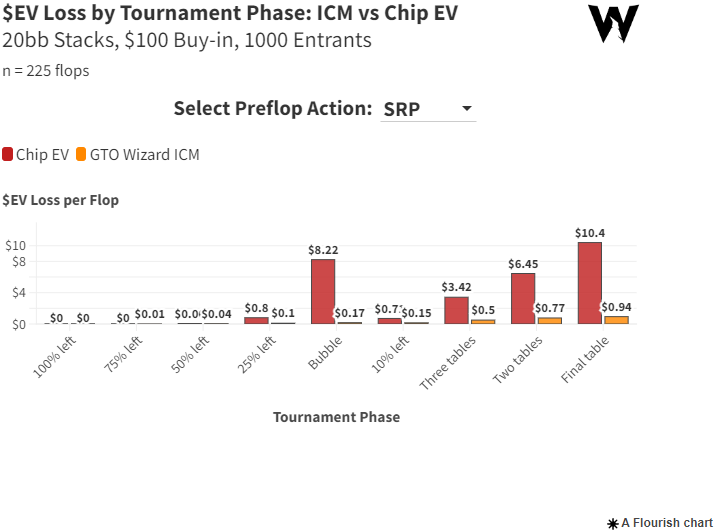
令人震驚的是，在泡沫階段（bubble）和決賽桌（final table），採用籌碼期望值（Chip EV）策略在每個翻牌上平均損失高達您初始買入的10%！在三倍下注底池（3-bet pots）中，採用籌碼期望值平均可能損失高達您買入的30%。請注意，我們僅鎖定了翻牌策略，這意味著Nemesis假設未來街的完美玩法（perfect play）。如果我們也測量轉牌（turns）和河牌（rivers），損失將更嚴重。即使在剩餘25%的玩家（15%進入獎金圈）時，我們也看到不可忽略的損失。這表明採用ICM意識策略（ICM-aware strategies）對您的錦標賽成功至關重要。

接下來，查看標記為GTO Wizard ICM的柱狀圖。這表示我們的ICM算法對近乎完美的CFR求解器（CFR solver）的表現。雖然我們的評估函數非常精確（我們的方法幾乎完美計算ICM值），GTO Wizard AI仍受限於之前的抽象（abstractions）——一次解決一條街，比CFR求解快數千倍。儘管如此，它在所有錦標賽階段的表現都非常出色，且僅需傳統求解器（solvers）時間的極小部分。

籌碼縮放錦標賽權益

在我們的ICM算法開發過程中，我們意識到一個標準化的指標（normalized metric）將易於在不同錦標賽階段、不同格式和起始底池大小之間進行比較。因此，我們發明了籌碼縮放錦標賽權益（Chip-Scaled Tournament Equity, CSTE）。

CSTE提供了一個可在不同格式和錦標賽階段比較的標準化價值。它特別適用於比較ICM和籌碼期望值（Chip EV）場景，或比較$EV與底池大小。例如，如果您的ICM獎金份額為5%，場上有1000個籌碼，您的CSTE將為50。請注意，$EV相對於棄牌（fold）= 0。

CSTE = Total_Chips × $EV / Remaining_Prizes

這裡我們可以看到與上述相同的圖表，使用CSTE/底池（Pot）進行標準化。這提供了一種衡量相對於底池大小的可剝削性（exploitability）的方法：

免費ICM計算器

我們創建了一個免費的公共工具，可以計算最多2048名玩家籌碼的ICM價值！輸入任何獎金和籌碼組合，根據獨立籌碼模型（ICM）計算每個籌碼量的錦標賽權益（tournament equity）和$EV！

我們的ICM計算器以及我們的GTO求解器（GTO Solver）具有許多節省時間的實用工具：

從常見多桌錦標賽（MTTs）導入獎金結構
按錦標賽ID搜索
自動籌碼分佈

GTO Wizard ICM – 我們的方法

我們的新算法使得計算ICM值同時實現高精度和高效率成為可能，這在過去被認為是不可能的。主要挑戰在於計算難度：精確計算（ICM）需要考慮所有可能的玩家排名，但隨著玩家數量增加，列舉這些排名很快變得難以處理。

為了支持30名或更多玩家的錦標賽，我們需要找到一種方法在不顯式列出這些排名的情况下考慮它們。最簡單的方法是使用抽樣方法（sampling method）：概率性地抽樣一些可能的排名，並根據這些樣本估計ICM值。然而，雖然這種方法可以處理大量玩家，但結果僅為估計值，精確度對我們來說不夠滿意。

受到抽樣方法理論方面的啟發，我們設計了一種新方法，顯著提高了精確度，同時保持高效。我們的成就是純粹的算法進展，這意味著它不依賴任何抽象（abstractions）、插值（interpolations）或機器學習技術。它純粹依賴於支撐ICM計算的理論數學。我們的方法提供精確的ICM值。這使其本質上多功能且穩健，能夠處理任何類型的輸入！

我們無法公開我們的確切方法。然而，我們已對傳統ICM計算方法進行了基準測試，以展示其速度和效率。

比較ICM計算方法

多年來，人們多次嘗試提高ICM計算的速度和效率。在本文中，我們將幾種著名方法與我們的方法進行比較。

ICM計算方法

Naive – 原始ICM計算方法。
Bitmask DP – Naive方法的優化版本，使用位掩碼動態規劃（bitmask dynamic programming）。這種方法需要顯著更多的內存，但可以處理更多玩家。
Monte Carlo – 一個重大突破，通過蒙特卡洛模擬（Monte Carlo simulation）允許解決大場多桌錦標賽。最初由Tysen Streib在傳奇的2+2論壇帖子中介紹，後來使用準蒙特卡洛技術（Quasi Monte Carlo techniques）優化，這種方法可以解決有數千名玩家的錦標賽。然而，該公式的收斂速度較慢。
HRC – Hold’em Resources Calculator – 一個具有專有ICM求解算法的商業求解器（solver）。這裡HRC的開發者提供了兩個基準：“HRC Fast”，專為大場設計；“HRC Full”，以運行時間換取更高精確度，用於較小場。
GTO Wizard ICM – 我們的突破方法。更快、更高效、更精確，允許近乎即時且精確地解決有數千名玩家的錦標賽場。

設置

首先，我們需要一種方法來計算我們設置的精確ICM值，且不依賴我們自己的模型或推斷。我們找到了一個特殊案例，基於1973年發表的論文《On a Model for Storage and Search》可以精確計算。此特定案例涉及籌碼線性增加而獎金線性減少：

stacks = [1, 2, 3, …, n]

prizes = [n, n-1, n-2, …, 1]

為了開發我們自己的ICM算法，我們使用各種特殊案例（例如上述案例）進行了廣泛測試，這些案例的真值（ground truth values）可使用針對每個案例量身定制的特定算法確定。我們發現的最差相對誤差不超過3e-9（0.0000003%），我們確認通常有超過12位數字匹配。同樣，我們的算法是通用的，不利用每個測試案例的任何特殊結構，而用於測試的邏輯則利用了這些結構。

結果

這裡我們比較精確ICM方法。以下表格顯示使用單個CPU線程（Ryzen 7950x）在一秒內可計算的最大玩家數量：

接下來，我們將我們的算法與兩個近似算法進行比較；Monte Carlo和HRC：

GTO Wizard ICM比其他近似方法精確數個數量級，同時僅需極少部分的計算時間。

完整基準

建模獎金

許多現代撲克錦標賽使用獎金（bounties）——淘汰另一名玩家可贏得的獎勵。創建一個新的最先進ICM計算模型還不夠。我們需要一種方法來估計錦標賽中的獎金權益（bounty equity），包括本手牌和未來手牌贏得獎金的可能性。

由於這不是一個小任務，我們在本文中詳細介紹了我們的完整方法：

獎金模型解釋：解決淘汰賽錦標賽

總結與致謝

解決最優多桌錦標賽（MTT）策略並非小事。籌碼效用的非線性性質意味著您的籌碼價值取決於錦標賽中的每個籌碼量。為了解決這個問題，我們必須應對各種工程挑戰：

創建一種全新方法，精確且快速地解決大場錦標賽的ICM值
計算獎金期望值（bounty EV）以及未來獎金期望值
將這些方法整合到我們現有的GTO Wizard AI框架中

最終結果是世界上最強大的工具，用於尋找最優錦標賽策略！

我想特別感謝我們的兩位工程師：Philippe Beardsell，我們的首席引擎開發者，以及破解新ICM公式的Wataru Inariba，感謝他們的辛勤工作。他們運行這些基準測試並指導了本文。我們還要特別感謝Adam Kelly提出CSTE並協助我們完成這個項目。在GTO Wizard，我們為雇用行業中最優秀的頭腦推動撲克理論前沿感到自豪。