多桌錦標賽中ICM何時變得重要？

獨立籌碼模型（Independent Chip Model, ICM）由M. Malmuth於1987年發明，是理解錦標賽撲克策略最重要的公式之一！但我們花了近35年才充分應用這個概念……

ICM擅長評估錦標賽籌碼，但直到最近，要在大規模多桌錦標賽（MTTs）中計算ICM幾乎是不可能的，特別是當許多玩家仍在場時。因此，在許多玩家仍在場的情況下，大家一直使用籌碼期望值（Chip EV）模型來評估錦標賽。撲克科學的最新進展現在允許我們在數百甚至數千名玩家仍在場時計算ICM。

這引出一個重要問題——在錦標賽中，ICM何時變得重要？何時值得切換到ICM解決方案？我們與Holdem Resources Calculator的創始人Helmuth合作進行了一系列實驗來找出答案

• 快速回顧 - 什麼是ICM？

• ICM與籌碼期望值（Chip EV）

• 方法論

  • 實驗#1 - 200人無限注錦標賽

  • 實驗#2 - 1000人無限注錦標賽

  • 實驗#3 - 更多策略

  • 實驗#4 - 不同籌碼深度

  • 實驗#5 - 解決誤解

• 這如何影響您的策略

• ICM的替代方案

• 結論

  
  

快速回顧 - 什麼是ICM？

獨立籌碼模型（ICM）是一個數學公式，將您的錦標賽籌碼從籌碼轉換為美元。ICM僅使用籌碼大小（stack sizes）來確定玩家在每個名次（1st、2nd等）的完成概率，然後根據這些名次的獎金分配錦標賽權益（tournament equity）。錦標賽權益只是您根據獎金結構、您在比賽中的位置和籌碼大小預期的獎池份額。

ICM與籌碼期望值（Chip EV）

籌碼期望值（Chip EV） = 最大化籌碼的策略

ICM = 最大化獎金的策略

這兩者並不相同。ICM的基本權衡是有時會犧牲籌碼以贏得更多美元。這是因為一個名為“風險溢價”（Risk Premium）的概念。在多桌錦標賽中，有時避免邊緣場景（marginal spots）以存活更久是值得的。損失對您的影響大於等量的籌碼增益。相反，籌碼領先者（chip leader）可以更激進地遊戲，因為他們預期其他玩家會更謹慎地玩。這種風險規避（risk-averse）動態在籌碼期望值策略中不存在。籌碼期望值策略僅最大化籌碼，無懼風險。

這種權衡是否合理？您應該為了獎金犧牲籌碼嗎？

繼續閱讀以了解答案。

方法論

這些實驗的目標是找出ICM在多桌錦標賽中何時成為重要因素。您應在何時從籌碼期望值模型（Chip EV model）切換到ICM模型？我們進行了一系列實驗來找出答案。我們模擬了多場錦標賽，不同策略組合相互競爭。

參賽者

• ICM 100%（純ICM）

• cEV 25% -> ICM 75%

• cEV 50% -> ICM 50%

• cEV 62.5% -> ICM 37.5%

• cEV 75% -> ICM 25%

• cEV 95.5% -> ICM-FT（僅決賽桌）

例如，參賽者（cEV 25% -> ICM 75%）在25%的玩家被淘汰前使用籌碼期望值策略，然後在剩餘75%的比賽中切換到ICM策略。每場錦標賽包含各策略組合的等量樣本。我們將統計他們的結果，查看切換到ICM的時點對結果的顯著影響。

實驗#1 - 200人無限注錦標賽

設置

• 200人多桌錦標賽無限注（Freezeout）

• 15%場內玩家獲獎

• 全下/棄牌（Push/Fold）

• 大盲（BB）= 平均籌碼的1/7

• 六種不同策略

• 每位玩家知道並適應彼此的策略

• 樣本量：500,000場錦標賽

我們模擬了一場200人的無限注錦標賽。這是一場全下/棄牌比賽，大盲標準化為錦標賽平均籌碼的1/7（平均籌碼 = 7BB）。每次有玩家被淘汰時更新。每位玩家知道並適應彼此的策略。

結果

以下圖表顯示了每個策略組合的平均投資回報率（ROI）。正如您所見，較早切換到ICM的玩家平均獲得更高的回報。

我們看到在場內剩餘50%到37.5%的玩家之間開始出現輕微下降。此時的損失超過統計顯著性（statistical significance），表明這種損失不是波動（variance）的結果。

這個結果令我們驚訝，因為它表明ICM在泡沫期（bubble）之前就成為重要因素。由於15%的場內玩家獲獎，泡沫期在剩餘15%的玩家時發生。然而，我們看到（cEV 75%/ICM 25%）儘管遠在泡沫期前切換到ICM，仍然損失了顯著價值。

在底部，我們看到（cEV 95.5%/ICM 4.5%）平均損失13%的買入。這種類型的參賽者使用籌碼期望值評估，試圖最大化籌碼，直到決賽桌才切換到ICM。

詳細結果

名次（Placements）

讓我們探索這些優勢從何而來。以下圖表顯示了每個策略組合的累計進入獎金圈（ITM）支付：

我們可以看到，較早切換到ICM的策略進入獎金圈的頻率更高。這是ICM整體贏得更多資金的主要原因。

我們可以進一步分解。以下圖表顯示每種策略在各名次的達成頻率：

我們可以看到，右邊的（cEV 95.5%/ICM 4.5%）出局（busting）頻率更高，名次較低。回想一下，這種策略組合直到決賽桌才使用ICM。

儘管如此，籌碼期望值策略獲得第一名的頻率高於其他策略。這正是我們預期的！ICM（和其他錦標賽權益模型）預測您獲得第一名的概率等於您在錦標賽中的籌碼比例。因此，最大化籌碼的策略會更頻繁地獲得第一名，但犧牲了進入獎金圈的名次。

相對於基準名次概率的比例變化（Proportional Change to Baseline Placements）

我們可以將上述名次與“基準”概率比較。以下圖表顯示相對於基準名次概率的比例變化。

• 基準概率（Baseline probability）= 隨機選擇時每位玩家的名次概率。

• 比例變化（Proportional change）= 實際名次概率 / 基準名次概率 – 1

換句話說，（cEV 95.5% / ICM 4.5%）策略比隨機選擇多18%的機會獲得第一名，但也多5.2%的機會出局。

期望值（Expected Value）

最重要的問題是期望值的問題。我們使用100美元買入，將每個名次頻率乘以其獎金的期望值，來查看策略在哪些地方獲得或損失價值。該錦標賽的獎池為20,000美元。

EV = Prize% × Prize pool × Placement frequency – $100 buy-in

看到每個名次在錦標賽中貢獻了多少資金是很有趣的。

將這個表格解讀為相對於基準期望值的變化更容易。ICM 100%到ICM 37.5%策略在除了第二名和第一名之外的所有地方都獲得期望值。這展示了ICM基本權衡的強大力量——在多桌錦標賽中，生存是王道。與此同時，ICM 25%及以下策略犧牲了泡沫期名次的期望值，以換取更高名次的更高期望值。

最後，我們可以繪製按策略分類的名次期望值圖表。

這裡的線條非常接近，只有一個主要例外——（cEV 95.5% / ICM 4.5%）策略。

這個圖表清楚地表明，籌碼期望值策略為了最大化籌碼並爭取第一名犧牲了很多資金。這個線條與其他線條的差異如此之大，以至於很難看到其他策略之間的較小差異。

實驗#2 - 1000人無限注錦標賽

複製（Replication）是科學家建立對結果價值的信心的重要方式之一。重複實驗和隔離變量是科學方法的核心原則之一。

在下一個實驗中，我們將使用更大的場次重複上述方法。我們應考慮這些結果可能是獎金結構或場次的偶然。

設置

我們使用與之前相同的設置，這次模擬1000人的無限注錦標賽。

• 1000人多桌錦標賽無限注

• 15%場內玩家獲獎

• 全下/棄牌（Push/Fold）

• 大盲 = 平均籌碼的1/7

• 六種不同策略

• 每位玩家知道並適應彼此的策略

• 樣本量：100,000場錦標賽

結果

與之前一樣，我們看到較早切換到ICM的策略平均表現更好。投資回報率（ROI%）的下降似乎在（cEV 50% / ICM 50%）和（cEV 62.5% / ICM 37.5%）之間開始。

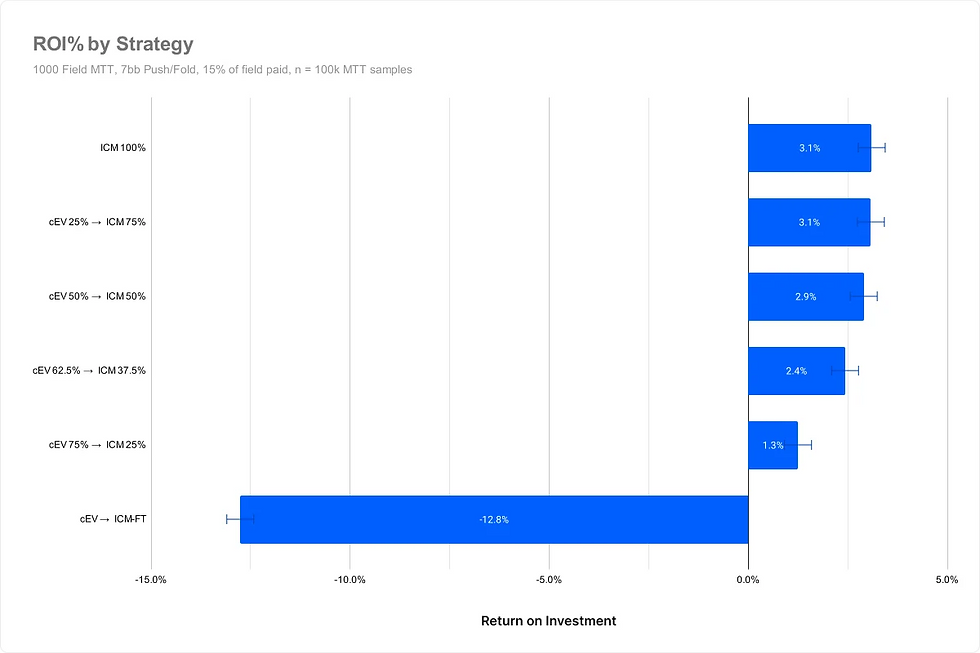
在兩個實驗中，ICM似乎在場內剩餘50%到37%的玩家之間對結果產生統計顯著的影響，遠早於15%的泡沫期。需要注意的是，置信區間（confidence interval）使我們無法斷言純ICM優於ICM 50%，儘管整體趨勢似乎與我們之前的結果一致。

詳細結果

名次（Placements）

這裡我們看到與之前相同的趨勢——較早切換到ICM的玩家整體進入獎金圈的頻率更高。

相對於基準名次概率的比例變化

期望值（Expected Value）

按名次的期望值

相對於基準名次期望值的變化

與200人實驗類似，我們看到較早切換到ICM的玩家更頻繁地進入獎金圈，以換取最高名次的稍低期望值。相反，較晚切換到ICM的玩家傾向於建立更大的籌碼並承擔更多風險，導致進入獎金圈的名次減少，以換取最高名次的更高期望值。

這裡我們可以看到相對於基準期望值的變化：

實驗#3 - 更多策略

我們首先運行這個模擬作為探索性模擬，以縮小使用的參賽者範圍。這些結果有助於將其他策略置於背景中。

設置

• 90人多桌錦標賽無限注

• 13名玩家獲獎

• 全下/棄牌

• 大盲 = 平均籌碼的1/7

• 九種不同策略

• 每位玩家知道並適應彼此的策略

• 樣本量：100,000場錦標賽

參賽者

• ICM 100%

• cEV 12.5% / ICM 87.5%

• cEV 25% / ICM 75%

• cEV 37.5% / ICM 62.5%

• cEV 50% / ICM 50%

• cEV 62.5% / ICM 37.5%

• cEV 75% / ICM 25%

• cEV 87.5% / ICM 12.5%

• cEV 100%

結果

我們看到與之前相同的趨勢——較早切換到ICM策略的玩家賺更多錢。

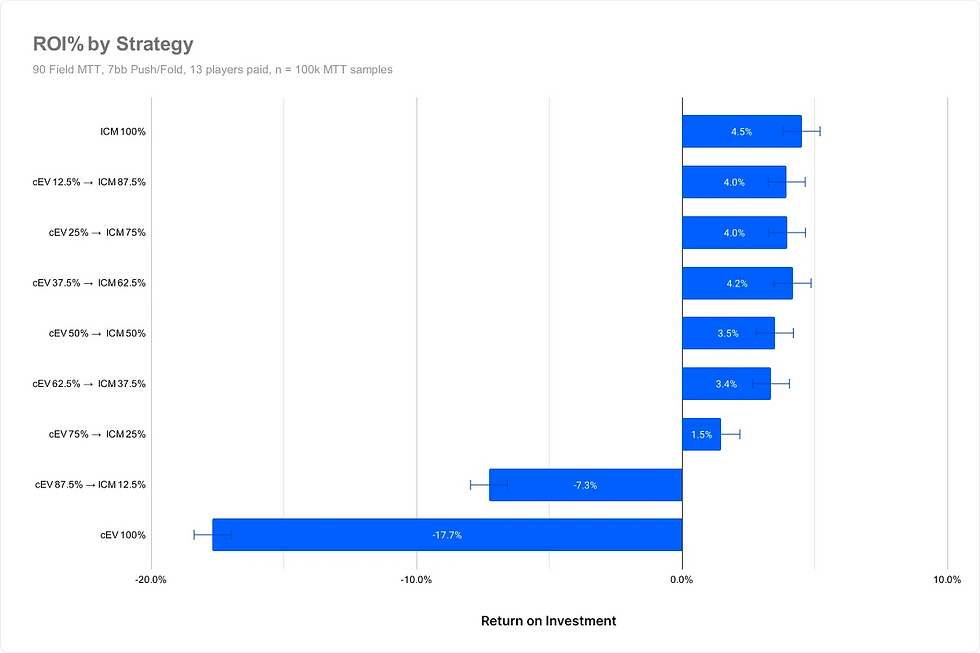
這些結果中有一些噪音，因為有更多策略上相似的策略。然而，總體趨勢保持一致。

值得注意的是，純籌碼期望值（cEV 100%）損失的價值遠多於前一個實驗，所有其他玩家的期望值（EV）與前次實驗相比都有所增加。這表明您的期望值是場內較差玩家數量的函數。

詳細結果

我們可以以統計信心說，（cEV 75% / ICM 25%）及以下策略正在損失價值。泡沫期在場內剩餘14.4%的玩家時發生，然而在剩餘25%的玩家時切換到ICM的玩家已經在損失。這強化了ICM在泡沫期前就具有統計顯著影響的觀點。為了簡潔起見，我們將跳過期望值和名次分析。

實驗#4 - 不同籌碼深度

我們之前的實驗都以7BB平均籌碼深度為特色。接下來，我們將在5BB和10BB之間變化籌碼深度，看看這對結果的影響。

設置

• 90人多桌錦標賽無限注

• 13名玩家獲獎

• 測試5BB、7BB、10BB全下/棄牌錦標賽

• 六種不同策略

• 每位玩家知道並適應彼此的策略

• 每項測試樣本量：500,000場錦標賽

5BB平均籌碼

詳細結果

7BB平均籌碼

詳細結果

10BB平均籌碼

詳細結果

不同籌碼深度的分析

在所有情況下，（cEV 62.5% / ICM 37.5%）及以下策略表現較差，具有統計顯著性。我們可以推測，由於全下/棄牌範圍收緊，10BB深度時的技能優勢縮小。然而，這可能只是波動（variance）。

實驗#5 - 解決誤解

許多玩家認為ICM假設錦標賽在計算後停止並支付獎金。事實並非如此。估計籌碼價值與停止錦標賽不同。這個誤解可能源於以下事實：

1. ICM常用於決賽桌交易（final table deals）。

2. ICM不考慮下一輪盲注增加或位置輪換。

ICM對策略不做任何假設，它不知道誰有位置，或“範圍”（range）是什麼意思。ICM僅估計籌碼名次概率（stack placement probabilities）。

在這個實驗中，我們將展示即使沒有玩家了解ICM概念，ICM仍然有效！

設置

這次，我們模擬兩組玩家：半籌碼玩家（half-stack players）和全籌碼玩家（full-stack players）。每個玩家都使用籌碼期望值（chip EV）策略，因此模擬中沒有人關心ICM。

• 兩組玩家，一組半籌碼，一組全籌碼

• 每個人都使用籌碼期望值策略

• 大盲 = 平均籌碼的1/7

• 200人場多桌錦標賽，15%場內玩家獲獎（與實驗#1相同的獎金結構）

• 全下/棄牌

• 100美元買入

• 樣本量：250,000場錦標賽

結果

這裡我們看到半籌碼和全籌碼玩家的模擬結果與ICM預測的結果相比。

例如，“前15%”表示一名玩家進入錦標賽前15%的頻率。“前50%”表示一名玩家進入前50%的頻率。ICM預測半籌碼組的錦標賽價值為67.74美元，全籌碼組為132.26美元。

讓我們看看這些預測與模擬結果的接近程度：

ICM預測每位玩家的期望值（EV），與模擬結果僅相差0.39美元。這些結果表明，獨立籌碼模型（ICM）是一個有價值且精確的錦標賽權益預測器，無論錦標賽中的玩家是否了解這個概念。結果還表明，ICM在最重要的地方——接近獎金較高的高名次——具有更強的預測力。

這如何影響您的策略

這些實驗的目的是找出ICM何時成為重要因素。我們可以在GTO Wizard中展示，即使在錦標賽的中途，策略也會顯著變化。

您可以使用GTO Wizard通過學習早期和中期多桌錦標賽的ICM策略來獲得對競爭對手的優勢。

以下GIF顯示了錦標賽中策略如何變化。這基於實驗#1中概述的200人獎金結構。

範例1：LJ首次加注（LJ RFI）

這裡我們看到20BB深度時的最優LJ開牌策略。為便於比較，所有玩家被分配對稱的20BB籌碼。頻率變化不大，但範圍的形狀（shape）變化顯著。

請注意，隨著錦標賽進展，開牌範圍變得多麼偏向阻斷牌（blocker-heavy）。隨著風險溢價（risk premium）增加，您的期望值更多來自偷盲（stealing the blinds）而非翻牌後遊戲（postflop play）。由於全下條件收緊（tightened stack-off conditions）和更高的風險溢價，翻牌後隱含賠率（implied odds）減少。因此，聽牌（drawing hands）被換成阻斷三倍下注（3bets）的手牌。

範例2：大盲防守（BB Defence）

ICM的影響在大盲最為明顯。這是另一個20BB對稱籌碼場景。看看隨著錦標賽進展，大盲面對LJ開牌時變得多緊！

即使在錦標賽中途，大盲的棄牌頻率（folding frequency）從19.6%變為35.5%。大盲範圍中的大多數手牌接近盈虧平衡，因此風險溢價的小變化對其防守有很大影響。

範例3：LJ面對按鈕位三倍下注（LJ facing BTN 3bet）

LJ開牌，按鈕位三倍下注，行動輪到LJ。這裡我們看到LJ的策略在錦標賽中如何變化。

請注意，隨著錦標賽進展，LJ的跟注頻率（calling frequency）減少。相反，LJ選擇全下/棄牌策略（shove/fold strategies），與按鈕位玩“ICM雞遊戲”（ICM chicken）。顯然，ICM對翻牌前和翻牌後策略有顯著影響。在GTO Wizard中查看這些策略變化讓我相信，我們的全下/棄牌實驗並未完全捕捉ICM在中期多桌錦標賽場景中的優勢。

ICM的替代方案

需要注意的是，ICM是一個不完美的模型。可以通過暴力計算（brute force）進行更精確的錦標賽評估，但僅適用於非常小的遊戲樹。Holdem Resources Calculator創始人Helmuth Melcher的這篇優秀論文比較了傳統ICM與替代模型。三個錦標賽權益模型與精確納什均衡策略（PI-CFR+）以及彼此對抗進行了比較。原始ICM方法被稱為“Harville”，有時稱為“Malmuth-Harville”，以其發明者命名。

模擬結果

以下部分的表格顯示了一名玩家使用基於指定權益模型的單手均衡策略，對抗另一名使用PI-CFR+策略的玩家的模擬結果。

Harville（ICM）和Robert的公式表現極佳，對完美策略僅損失1%的買入。需要注意的是，Robert對精確策略的損失更少，但當Harville（ICM）與Robert公式對抗時，Harville勝出。

我們偏好ICM的原因是它更有效率。原始ICM計算可以擴展到即時評估數千名玩家！

ICM有一些普遍的局限性，我們在此概述。主要弱點是ICM忽略了下一輪盲注增加、位置輪換（除非使用FGS）、技能優勢（skill edge）和位置（position）。一般來說，ICM傾向於低估籌碼領先者的優勢。但總體而言，即使在發明35年後，ICM仍然是一個極其強大的公式。

結論

這些實驗的目的是找出ICM在多桌錦標賽中何時成為重要因素 ⚖ 為了測試這一點，我們模擬了數百萬場多桌錦標賽，參賽者在比賽的不同時點從籌碼期望值模型（chip EV models）切換到ICM模型。

• 我們測試了多種錦標賽結構和場次大小

• 我們測試了多種籌碼深度

• 我們展示了即使沒有玩家使用ICM，ICM的預測能力

• 我們展示了即使在錦標賽中途，求解器（solvers）策略也顯著變化

我們的結果一致發現，較早切換到ICM的玩家表現優於較晚切換的玩家。

在比賽中途前切換到ICM的策略看到了回報的穩定增加，但增益相對較小且在誤差範圍內。我們以高信心展示了ICM在15%獎金結構下，場內剩餘50%到37%時對結果有統計顯著的影響。我們可以推測，切換到ICM的“最佳時機”（sweet spot）大約在泡沫期的三倍時發生。現在應該清楚，ICM在泡沫期前對策略有顯著影響。

Holdem Resources Calculator

我們衷心感謝Holdem Resources Calculator（HRC）的創始人Helmuth Melcher進行這些模擬並在實驗中提供指導。