平分牌面的荒誕博弈論
- Tombos21

- 2025年7月17日
- 讀畢需時 7 分鐘
在撲克中,“平分牌面”(chopped board)是指公共牌構成兩位玩家範圍(ranges)中大多數手牌的最佳五張牌組合的情況。這通常被稱為“玩牌面”(playing the board)。平分牌面導致了引人入勝、常常違反直覺的策略。本文將深入探討平分牌面的荒誕數學。
在開始之前,請觀看Qing Yang的這段視頻,了解更多關於“玩牌面”理論的內容。
案例1)所有手牌平分
平分牌面最明顯的例子是像AKQJT彩虹(rainbow)或AAAAK這樣的牌面。任何玩家能形成的最強手牌已經在牌面上。因此,任何不涉及棄牌(folding)的策略都應該是好的。然而,如果這是一場現金遊戲(cash game)且涉及抽水(rake),會發生什麼?
100大盲(bb)小盲(SB)對大盲(BB)單人加注底池(single-raised pot)。他們到達河牌(river),底池有12大盲,有效籌碼後面94大盲。牌面是A♠ K♥ Q♦ J♣ T♠。每手牌都是順子(straight),且每手牌都平分(chops)。
在NL50現金遊戲中,小盲的最佳策略是什麼?在NL500現金遊戲中呢?
NL50抽水結構:5%抽水,4大盲上限
NL500抽水結構:5%抽水,0.6大盲上限
在NL50例子中,我們的任何下注(bet)都會被跟注(called),導致兩位玩家支付更多抽水。因此,最佳策略是範圍檢查(check-range)並嘗試在不向莊家(house)捐更多錢的情況下攤牌(showdown)。
然而,在NL500例子中,我們已經達到了抽水上限(0.6大盲上限 / 5% = 12大盲最大抽水底池)。因此,我們下注不會支付額外的罰款。此外,下注允許大盲犯錯(棄牌,folding),因此下注弱主導檢查(weakly dominates checking)。因此,小盲全下(shoves)其整個範圍!

囚徒困境
好吧,如果我們支付更多抽水或下注更大,會發生什麼?是否可以利用抽水對抗對手,迫使他們棄牌?令人驚訝的是,答案是肯定的!
《每日一劑GTO #305》探討了這個玩具遊戲(toy game)的奇特變體。如果上述NL50場景是一個跛入底池(limped pot)並檢查到河牌,最佳策略竟然是將99大盲全下到2大盲的底池中,這是一個4950%底池大小的全下(pot-sized shove)。
這個全下迫使大盲棄掉所有牌。如果大盲跟注,他們贏得一半底池(1大盲),但支付2大盲的抽水。因此,最高期望值(EV)的決定是放棄底池!

第一個全下的玩家應該贏得底池。滑稽的是,在真實遊戲中,大盲的最佳策略是搶先在小盲行動前非輪次全下(shove out-of-turn order)!但假設您在線上遊戲,無法這樣做。
面對這個全下,棄牌是最佳策略嗎?大盲可以“惡意跟注”(spite call),迫使雙方支付2大盲的抽水。這就是囚徒困境(Prisoner’s Dilemma)出現的地方。大盲是否應該偶爾惡意跟注以阻止小盲欺凌他們?
下表顯示了所有策略對的期望值(payoff table)。請注意,由於抽水,任何涉及雙方全下的策略都會導致負回報。理想情況下,雙方都檢查到底池(check down the pot)。然而,一方可以試圖迫使另一方棄牌以獲得優勢。這是囚徒困境的定義,但在此場景中,位置內玩家(IP player)知道對手的行動。

1981年,Robert Axelrod舉辦了一場比賽,尋找重複囚徒困境遊戲(Repeated Prisoner’s Dilemma)的最佳策略。結果顯示,一個名為“以牙還牙”(Tit For Tat)的簡單策略最強。這個策略從合作開始,如果對手背叛則報復。它報復很快,但也很快原諒。然而,這個策略是為重複遊戲設計的。在撲克中,平分場景發生得如此罕見,人類的短期記憶掩蓋了“惡意跟注”或設置報復威脅的意義。
案例2)部分手牌平分
案例2是這個遊戲更有趣的版本。在這種場景中,一些手牌平分,但其他手牌能擊敗平分。例如,AKQJT牌面但可能有同花(flushes)。
讓我們從一個簡單的玩具遊戲開始。有三類手牌:誘捕牌(Traps)、價值手牌(Value Hands)和平分牌(Chops)。反派(Villain)檢查一組平分牌和少量堅果誘捕牌(nutted traps)。英雄(Hero)有擊敗平分牌但輸給誘捕牌的價值手牌。
Traps > Value > Chops

在這個玩具遊戲的原始版本中,英雄需要找到最佳下注大小(bet size)以從詐唬攔截牌(bluff-catchers)中提取最大價值,同時不向反派的誘捕牌捐太多。然而,在這個遊戲中,沒有詐唬或詐唬攔截牌。所有平分牌彼此平分底池。這種動態改變了一切。
詐唬頻率
在“典型”的極化對詐唬攔截牌玩具遊戲中,您需要的詐唬數量由給出的底池賠率(pot odds)決定。如果您過度詐唬(over-bluff),反派可以通過總是跟注獲得期望值(EV);如果您低詐唬(under-bluffing),他們可以通過棄掉所有詐唬攔截牌剝削您。
目標 – 使反派的平分牌在跟注和棄牌之間無差別(indifferent)。
在平分牌面上,您的目標相同,使他們在跟注和棄牌之間無差別。然而,在這種情況下,跟注的獎勵(reward)小得多。當他們正確跟注時,他們只贏得一半底池(相比典型詐唬攔截場景中贏得整個底池加上您的下注)。這意味著跟注的獎勵是固定的,但跟注的風險(risk)仍隨下注大小縮放。
下圖顯示了在平分牌面上與典型極化場景相比,您應該多頻繁地詐唬。
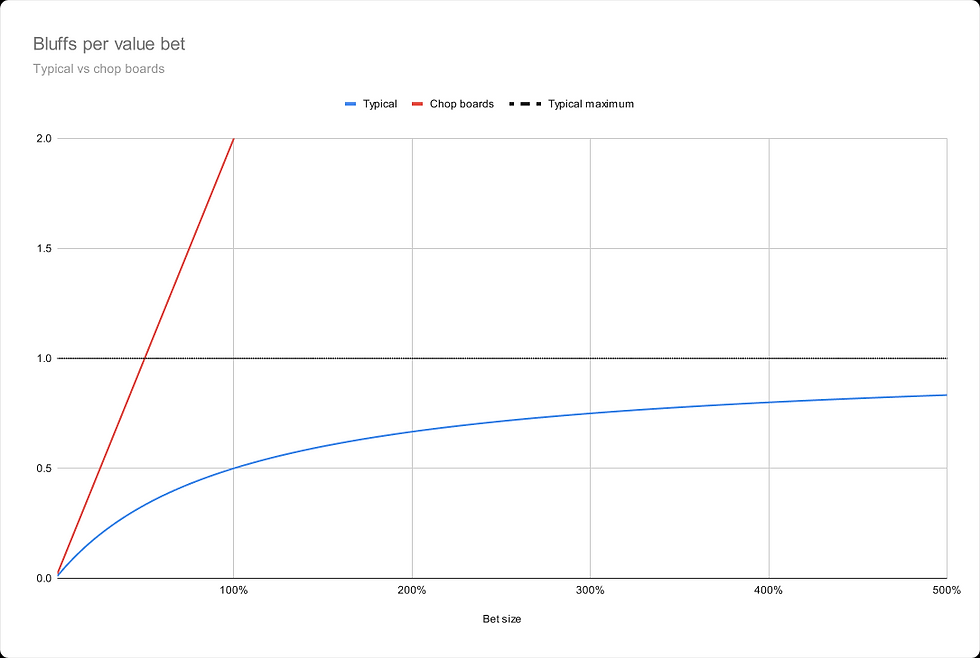
請注意,與傳統極化場景相比,詐唬頻率(bluffing frequency)急劇上升。在傳統極化場景中,您的每價值下注(value bet)的詐唬數量等於Alpha方程,s / (s+1),其中‘s’是下注/底池(bet/pot)。在平分牌面上,您的每價值下注的詐唬數量等於2s,是下注大小的兩倍。主要結論是,在平分牌面上,您應該比極化場景更頻繁地用價值手牌詐唬。
跟注頻率
反派應該多頻繁地跟注下注?這是一個出乎意料複雜的問題。我們知道,如果我們下注太大,反派會棄掉除誘捕牌(traps)外的所有牌。但較小的下注大小更難計算。要解決這個問題,我們首先需要問MDF和Alpha等方程試圖計算什麼。防守玩家的目標是使我們的平分牌在詐唬和檢查回來(checking behind)之間無差別。
目標 – 使英雄的平分牌在詐唬和檢查之間無差別。
為此,我們將每個行動的期望值(EV)設為相等,然後求解跟注頻率(calling frequency)。
EV (Check Chop) = EV (Bluff Chop)
以下解釋了如何推導平分牌面上的防守頻率:
檢查回來(checking behind)平分牌(chop)的期望值(EV)是反派(villain)範圍中誘捕牌(traps)比例的函數。
EV (Check Chop) = (1 – traps%) * pot / 2
詐唬(bluffing)平分牌的期望值更為複雜。期望值是我們被跟注(called)時的權益(equity)以及反派棄牌(folds)的頻率的函數,這兩者都取決於我們的投注大小(bet size)。
讓我們先用文字寫出公式:
EV (Bluff Chop) = (Fold% × pot) + Call% {(How often we get called by chop × 0.5 pot) – (How often we get called by trap × bet size)}
定義變量
跟注百分比(Call%) = c
棄牌百分比(Fold%) = 1 – c
反派範圍中的誘捕牌比例(Traps% in villain’s range) = t
下注/底池(Bet / Pot) = s
跟注範圍中的誘捕牌比例(Traps% in calling range) = t/c
跟注範圍中的非誘捕牌比例(Non-traps% in calling range) = 1-t/c
代入變量並簡化:
EV (Bluff Chop) = (1 – c) + c ( (1 – t/c) / 2 – st/c)
將檢查平分牌的期望值(EV (Check Chop))等於詐唬平分牌的期望值(EV (Bluff Chop)),並求解c:
(1-t)/2 = 1-c + c((1-t/c)/2 – st/c)
c = 1 – 2st
反派永遠不會棄掉誘捕牌,無論我們下注多大,因此實際的MDF公式變為:
Call% = Max (t, 1 – 2st)
與“典型”極化對詐唬攔截牌玩具遊戲中的曲線MDF不同,在平分牌面上,MDF是一條相對於範圍中誘捕牌數量向下傾斜的直線。如果您下注足夠大,他們只需防守誘捕牌,導致防守頻率變平並保持不變。

按下注大小的期望值曲線
這些期望值圖表顯示了英雄的總期望值(以底池百分比計),根據他們的下注大小。為簡單起見,我們假設反派只能跟注或棄牌。在典型的極化對詐唬攔截牌玩具遊戲中,最高期望值的下注大小取決於反派有多少誘捕牌。我們在《如何解決玩具遊戲》文章中討論了這一點。
在沒有誘捕牌的場景中,英雄的最優河牌策略是全下(或在早期街以幾何下注,geometric bet,在河牌全下)。如果反派有誘捕牌,英雄應下注較小,以避免防守範圍過強。以下圖表假設英雄開始時有50%的價值手牌和50%的詐唬(然後根據下注大小選擇最優詐唬或放棄)。
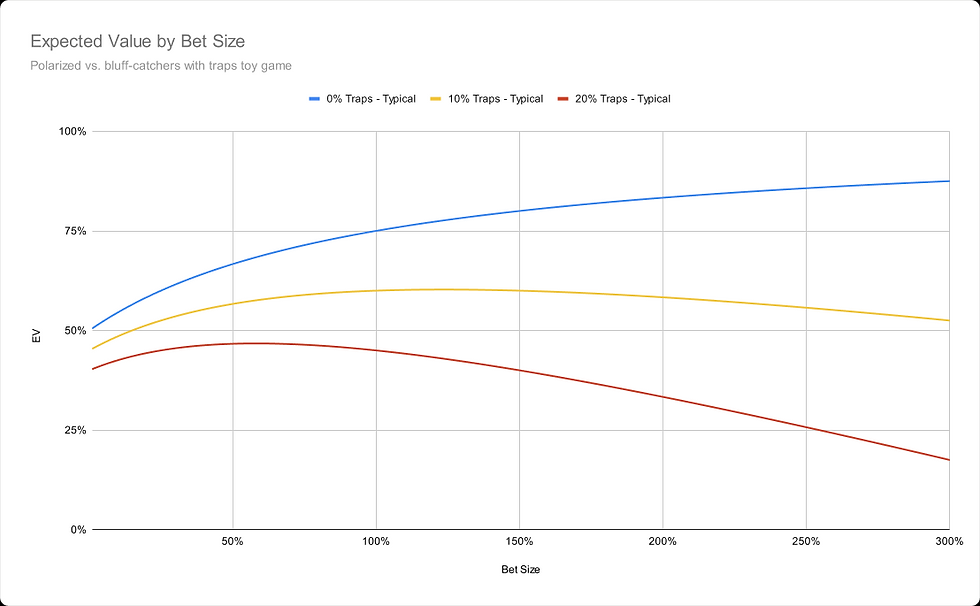
在我們的平分玩具遊戲場景中,情況有所不同。下注的期望值在英雄用完詐唬時達到一個“拐點”(inflection point)。從那時起,加大下注只會降低價值下注的期望值。
英雄應為每個價值下注有X%的詐唬,其中X等於下注大小的兩倍。例如,當下注150%底池大小時,英雄應為每個價值下注詐唬3個平分牌,以使反派對其“平分攔截牌”(chop-catchers)在跟注和棄牌之間無差別。
下圖顯示了英雄按下注大小的期望值。這裡我們假設英雄開始時有25%的價值手牌和75%的平分牌。在s = 150%時,我們用完了詐唬,因此這設定了理論最大下注大小。然而,如果反派至少有我們價值下注一半的誘捕牌,則最優下注大小可能變小,如下圖紅線所示,反派範圍中有20%的誘捕牌。

結論
上面的玩具遊戲相對簡單。擁有誘捕牌的玩家被動化(pacified),且沒有手牌相互阻斷(block)。在真實遊戲中,涉及的變量遠更多。玩家可以加注和再加注。有時您可能擁有的唯一堅果手牌(nutted hands)會阻斷對手擁有這些手牌。
然而,我們仍能從這個平分牌面玩具遊戲中學到幾個關鍵要點:
在範圍中大部分為平分牌的牌面上更頻繁地詐唬。
您常常會用完詐唬,因此應在這些牌面上範圍下注(range-bet)。
通常這意味著您也應在這些牌面上更廣泛地跟注。
您應整體防守多廣取決於您有多少誘捕牌(traps)。
注意抽水結構(rake structure)。如果您無法讓他們棄牌,則不值得無端增加底池並支付更多抽水。




留言