撲克組合數學入門指南
- Tombos21

- 2025年7月13日
- 讀畢需時 5 分鐘
組合數學(Combinatorics)是一個用來評估任何特定手牌可能“組合”(combos)數量的專業術語:特定等級和花色的兩張牌的組合。它讓我們能夠回答諸如在特定情況下可以持有多少不同版本的AK、哪些手牌更適合作為詐唬攔截牌(bluff-catchers)等問題。
組合計數基礎
手牌矩陣(The Hand Matrix)
在德州撲克(Texas Hold’Em)中有1326種可能的起始手牌組合。它們通常以一個常被稱為手牌矩陣(hand matrix)的網格表示。
僅看手牌矩陣,很容易誤以為口袋對(pocket pairs)佔可能手牌的13/169,同花(suited)和非同花(offsuit)手牌各佔78/169。通過查看網格並對應每個手牌類別的方格進行求和,我們會得出上述答案。然而,這假設所有方格彼此相等。雖然在幾何上確實如此,但在組合數學上並非如此。
實際上:
每個口袋對有6種組合:
A♠A♥, A♠A♦, A♠A♣, A♥A♦, A♥A♣, A♦A♣
每種同花手牌有4種組合:
A♠K♠, A♥K♥, A♦K♦, A♣K♣
每種非同花、非對子手牌有12種組合:
A♠K♥, A♠K♦, A♠K♣, A♥K♠, A♥K♦, A♥K♣, A♦K♠, A♦K♥, A♦K♣, A♣K♠, A♣K♥, A♣K♦
這得出結論:有78個口袋對(6種組合 × 13個方格)、312個同花手牌(4種組合 × 78個方格)和936個非同花、非對子手牌(12種組合 × 78個方格)。
想在實際遊戲中練習組合計數嗎?GTO Wizard的遊戲模式(Play Mode)讓您通過玩手牌並在之後審查範圍(ranges)來測試您的理解,提供了一個實用的方式來強化這些概念。
牌面矩陣(The Card Matrix)

死牌(Dead Cards)
上述比例適用於翻牌前(preflop),但在存在“死牌”(dead cards)時會失效。死牌指的是已知不在玩家手中的牌。最常見的例子是當翻牌(flop)發出時。翻牌上的牌是死牌,因為任何玩家都不可能持有它們。
計數組合的最簡單方法是將未見牌的數量相乘。讓我們通過一些例子來熟悉:
按鈕位(BTN)開牌,大盲(BB)跟注,翻牌是AK2:

按鈕位有多少種AQ的組合?

請注意,其中3/12是AQs,9/12是AQo。
同花:A♦Q♦, A♥Q♥, A♣Q♣, A♠Q♠
非同花:A♦Q♥, A♦Q♣, A♦Q♠, A♥Q♦, A♥Q♣, A♥Q♠, A♣Q♦, A♣Q♥, A♣Q♠, A♠Q♦, A♠Q♣, A♠Q♥
按鈕位有多少種AA的組合?
口袋對使用略不同的公式。我們從AA的6種組合開始。如果翻牌是A♠K♥2♦,A♠不再在我們的範圍中。我們的AA組合從6減少到3:沒有A♠A♥, A♠A♦, A♠A♣, 有A♥A♦, A♥A♣, A♦A♣。
我們可以使用以下公式計算口袋對的可用組合數:

其中a = 口袋對等級的可用牌數量。在此場景中,我們輸入a = 3,因為有3張可用的A(A♥, A♦和A♣)。(3 * (3-1))/2 = 3種AA的組合。
另一種說法是“3選2”。
按鈕位有多少種AKs的組合?
同花手牌可以直觀計數,不需要公式。在A♠K♥2♦牌面上,AKs的可用組合數從4減少到2,因為牌面上的A♠和K♥:A♠K♠, A♥K♥, A♦K♦, A♣K♣。
我們可以使用以下公式計算AK的總組合數:

其中a = 一張牌等級的可用牌數,b = 另一張牌等級的可用牌數。
在A♠K♥2♦牌面上,有3張可用的A(A♥, A♦, A♣)和3張可用的K(K♥, K♦, K♣)。因此我們輸入a = 3,b = 3,得出結果為9。知道其中2種是同花組合,剩餘7種是AKo的組合。
其他牌移除範例
當公開信息使某些手牌不可能持有時,存在死牌。然而,還存在其他更微妙的牌移除形式。一個重要的形式是阻斷牌(blockers)。這是當一名玩家利用他們手牌或私人死牌提供的私人信息,通過組合數學縮窄對手的範圍。
簡單阻斷牌範例
阻斷牌(Blockers)是撲克策略中至關重要的一部分,可能決定邊緣決策的成敗。通過從玩家的範圍中排除特定組合,您可以改變他們的行動頻率(action frequencies)和價值與詐唬比率(value to bluff ratios)。
讓我們檢查一個簡單的例子,展示如何利用這個效應:


[6人現金遊戲,500NL,100BB]
按鈕位開牌到2.5BB,大盲防守。大盲檢查-跟注(check-calls)33%翻牌續注(c-bet),125%轉牌續注,並在J♠5♥2♠K♦8♠牌面上面對85%的河牌續注。以下哪些手牌可以有利可圖地跟注?
A) K♠9♥
B) K♥9♠
C) K♣T♣
D) A♥5♦
答案
A) K♠9♥

大盲需要至少31.5%的權益(equity)來有利可圖地跟注(計算您的底池賠率,pot odds)。通過“阻斷”價值手牌(value hands),K♠9♥比其他答案對按鈕位的範圍有更多權益,可以進行這個跟注。按鈕位在這個河牌價值下注(value bets)兩對及以上,並以A高及以下詐唬(bluffs),因此所有列出的手牌都是詐唬攔截牌(bluff-catchers)。對手範圍中的價值與詐唬比率根據我們持有的牌而變化!
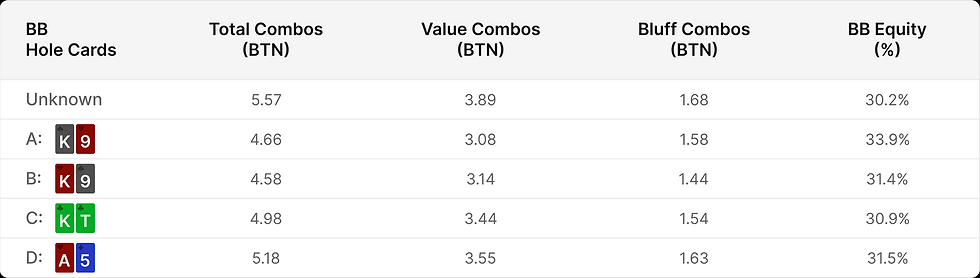
大盲僅在持有K♠9♥時對按鈕位的範圍有超過31.5%的權益,使其成為唯一有利可圖(+EV)的跟注。
策略頻率與實際頻率
儘管阻斷牌改變了範圍行動頻率(range action frequencies),求解器(solvers)(包括GTO Wizard)不會在它們的策略頻率(strategic frequencies)中顯示這種效應的影響。這導致策略頻率與實際頻率(actual frequencies)之間的差異。這在同花牌面(flush boards)上表現得尤為明顯:

[6人現金遊戲,500NL,200BB]
中間位置(HJ)開牌到2.5BB,大盲防守。大盲檢查-跟注130%的續注,轉牌檢查通過(checks through),並在Q♠J♠4♥7♦2♠牌面上對61%的河牌下注檢查-全下(check-shoves)(407%)。
儘管策略頻率窗口聲稱中間位置跟注19.8%的時間(總共5.51組合中的1.07組合),實際上他們只跟注13.8%(總共3.78組合中的0.52組合)。
19.8%的頻率包括“幽靈”組合(ghost combos):由於對手的阻斷牌而無法存在的組合。

大盲僅全下包含A♠的手牌,然而,中間位置的19.8%跟注頻率包括許多A♠手牌。移除這些後,跟注頻率變為13.8%。
這並不意味著策略不正確。期望值(EV)計算考慮了這種效應。這只是解讀和顯示數據的問題。我們是想檢查策略頻率還是實際頻率?一些求解器有開關,允許您在這兩個視圖之間切換。
牌堆積(Card Bunching)
我們將檢查的最後一個牌移除效應是牌堆積(card bunching)。玩家在翻牌前傾向於更頻繁地棄掉低牌(low cards)而非高牌(high cards)。因此,當許多玩家已經棄牌時,剩餘玩家和牌庫偏向高牌。
在3人桌上,按鈕位首先行動,他們範圍中的每組組合可能性相等。在6人桌上,當幾個玩家已經棄牌時,情況並非如此。這種牌移除影響了所有待行動玩家的範圍和策略、頻率以及牌面出現概率(runout probabilities)。

這意味著當輪到按鈕位行動時,他們更可能持有高牌。這可能改變按鈕位的實際開牌頻率(actual opening frequency),即使他們不改變策略開牌頻率(strategic opening frequency)。
讓我們可視化這個效應。以下動畫顯示在幾個玩家棄牌後,牌庫中從2到A的牌密度。請記住,他們更可能棄掉低牌,因此牌庫中剩餘的牌(以及尚未行動的玩家範圍)更偏向高牌(top-heavy)。

一般來說,由於牌堆積導致的牌移除影響不大,儘管這取決於具體場景。作為一篇入門文章,我們不會詳細涵蓋這個效應。如果您想了解更多關於牌堆積效應的內容,請查看HRC的這篇文章。
結論
德州撲克有1326種可能的起始手牌組合,包括78個口袋對(pocket pairs)、312個同花手牌(suited hands)和936個非同花、非對子手牌(unpaired, offsuit hands)。其中一些組合可能被牌面或玩家的手牌和範圍阻斷(blocked),進一步減少可用組合數。制定策略時應考慮並優化這一點。
有三個關鍵的牌移除效應:死牌(dead cards)、阻斷牌(blockers)和牌堆積(card bunching);每個都有其獨特屬性。
如果您想挑戰自己的技能,試試這個組合數學撲克難題!
如果從本文中您能學到一件事,那就是不要太線性地思考您的手牌,而要更多地考慮您面對的範圍,以及這如何影響您使用阻斷牌的方式。祝您在牌桌上好運!




留言