求解器如何運作

博弈論最優（Game Theory Optimal, GTO）求解器（solvers）是一種計算最佳撲克策略的算法。但這些求解器究竟如何運作？什麼使它們的策略成為“最佳”？

本文將深入探討求解器的運作方式、它們實現的目標以及它們的局限性。

求解器的目標

在深入探討之前，請先閱讀以下兩篇文章。本文旨在提供對求解器運作方式的深入理解，如果沒有一些基本的前提知識，可能會感到不知所措。如果您是求解器的新手，請先閱讀以下內容，然後返回本文：

• 什麼是撲克中的GTO？

• GTO的目標是什麼？

正如在《什麼是撲克中的GTO？》和《GTO的目標是什麼？》中所討論的，GTO的目的是實現一個不可剝削的納什均衡（Nash Equilibrium）策略。

納什均衡是一種狀態，在此狀態下，沒有玩家可以通過單方面改變策略來獲得更好的結果。這意味著如果每個玩家公開他們的策略，沒有人會有動機改變策略。這常被描述為撲克策略的“聖杯”（Holy Grail）。但這實際上並不是求解器的設計目標。事實上，求解器對“納什均衡”毫無概念。

求解器只是最大化期望值（EV-maximizing）的算法。

求解器中的每個代理（agent）代表一名玩家。該玩家只有一個目標：最大化金錢。問題在於其他代理玩得完美。當您迫使這些代理對抗彼此的策略時，它們會來回迭代，剝削（exploit）彼此的策略，直到達到一個雙方都無法再改進的點。這一點就是均衡（equilibrium） 。

GTO是通過讓剝削性算法（exploitative algorithms）相互對抗，直到雙方都無法進一步改進來實現的。

如何解決GTO

• 為每位玩家分配一個均勻隨機策略（每個決策點的每個行動等可能）。

• 計算每手牌在遊戲樹（game tree）中對對手當前策略的遺憾值（regret，期望值損失，EV loss）。

• 改變一名玩家的策略以減少其遺憾值，假設對手的策略保持固定。

• 返回步驟2，重新計算遺憾值，然後改變對手的策略以減少遺憾值。

• 重複直到達到納什均衡。

這些循環中的每一個被稱為一次迭代（iteration）。所需迭代次數從幾千到幾十億不等，具體取決於遊戲樹的大小和抽樣方法（sampling method）。

步驟1）定義遊戲空間

輸入

撲克太過複雜，無法直接解決；我們需要使用子集（subsets）和抽象化（abstractions）來縮減遊戲空間（gamespace），使其可計算。

一般來說，運行求解器需要定義以下參數：

• 下注樹（Betting tree）。

• 所需精確度（Required accuracy）。

• 起始底池和籌碼大小（Starting pot and stack sizes）。

• 起始範圍（postflop solvers）。

• 公共牌（Board cards，postflop solvers）。

• 翻牌後牌抽象化，例如牌分桶（card bucketing）或神經網絡（NNs，preflop solvers）。

• 對效用函數的修改，例如抽水（rake）或ICM。

下注樹複雜性

我們需要定義可用的下注大小（bet sizes）以縮減遊戲樹的規模。在進入算法之前，我們需要理解“下注樹”是什麼樣子。求解器在您提供的參數內運行。如果您給求解器一個非常簡單的遊戲樹，您會產生較不複雜的策略，但請記住，求解器會剝削（exploit）您遊戲樹的局限性。

求解器將生成一個包含給定下注結構內所有可能路線（lines）的“樹”。該樹中的每個決策點包含一個“節點”（node）。例如，非位置（OOP）面對1/3底池大小的下注是一個“節點”。樹中的節點數量定義了樹的大小。每個節點都需要優化。

一個極其簡單的樹，如下所示，有696,613個單獨節點需要優化。

GTO Wizard使用的較複雜的樹包含約87,364,678個節點。

如您所見，複雜性使遊戲樹呈指數增長。上面複雜的樹每個節點使用4-5倍的下注大小，但它比簡單樹大125倍且更難解決。這仍然是對真實遊戲空間的重大簡化。

求解器最困難的問題之一是在當前技術限制內優化下注樹以產生穩健的策略。我們只能讓樹大到一定程度，否則因其規模而無法解決。我們也只能讓樹小到一定程度，否則求解器開始剝削該樹的局限性。我們正在研究找到簡化下注樹的算法，以使學習撲克更容易！這些解決方案將為每個場景找到最佳下注大小。

GTO Wizard有許多不同類型的解決方案，例如包含多達19種大小的複雜解決方案（complex solutions）和僅有幾種大小的簡單解決方案（Simple solutions）。最終，我們發現最好從複雜的樹開始，然後通過移除不常見的路線將其修剪成更小、更易管理的樹。

節點鎖定（Nodelocking）

GTO Wizard計劃在2023年添加節點鎖定（nodelocking）和即時解決（real-time solving）功能！這個強大功能將用於探索剝削性策略（exploitative strategies）和底層因果原則（cause > effect principles）。

節點鎖定是在遊戲樹中的某個節點固定一名玩家的策略。我們強制該玩家以特定方式遊戲。節點鎖定通常用於開發剝削性策略！例如，如果您強制其在翻牌範圍下注（rangebet the flop），對手玩家將最大化剝削該策略。然而，重要的是要記住，兩位玩家會在之前和之後調整以適應該鎖定節點。轉牌（turn）和河牌（river）策略會改變。

如果您強制求解器玩得不好，它會在之前和之後的節點進行校正以最小化損失。

鎖定單個節點並讓求解器繞過該缺陷的過程被稱為“最小剝削策略”（minimally exploitative strategy）。我們不是在模擬整個樹的某個漏洞，而僅是樹中的特定點。

更複雜的節點鎖定是可能的。例如，一些求解器允許您在一個節點鎖定特定組合的策略（同時讓其他組合調整策略）。也可以鎖定多個節點以重現並剝削對手策略中的更大趨勢——但現代工具無法有效適應多街節點鎖定。

步驟2）解決遊戲樹！

我們已經定義了遊戲樹。現在是時候解決它了！首先，我們需要理解求解器如何計算策略的期望值（EV）。

求解器如何計算期望值？

讓我們想像上面的遊戲樹。每個點代表一個節點或決策點。我們如何知道每手牌在每個節點生成的期望值？

這個過程對電腦來說很簡單。首先，我們定義終端節點（terminal nodes，又稱葉節點，leaf nodes）。這些是手牌終止的點，要么因為有人棄牌（folded），要么因為手牌進入攤牌（showdown）。

每個終端節點被分配一個概率（p）和一個價值（x）。我們範圍中的每手牌（i）在到達每個終端節點時生成不同的價值和概率。我們將每個終端節點的價值和概率相乘並求和，得出總期望值。每個節點的價值定義為我們贏得的總底池減去我們投入該底池的金額。

• 從一對策略開始。

• 根據我們的策略和對手的策略，我們的手牌到達每個終端節點的頻率為p。

• 每個終端節點的價值為x。

• 每個終端節點的x*p之和給出我們的期望值（EV）。

• 對每手牌在每個節點進行此計算。

E [X] = Σxip(xi)

xi = X採取的值

p(xi) = X採取值xi的概率

求解器幾乎可以即時進行此計算。在求解器出現之前，像CREV這樣的程序用於計算期望值。限制在於用戶必須定義每個節點的策略。因此，通常我們將後續節點簡化為純粹權益計算（pure equity calculations），這極不準確。

在GTO Wizard中，我們可以觀察每手牌在每個點的期望值。例如，這是一場NL50現金遊戲中的按鈕位對大盲單人底池（BTN vs BB SRP）。我們可以看到每手牌的整體期望值（使用策略下拉菜單），並將鼠標懸停在任何單手牌上可顯示我們可能採取的各種行動的期望值：

遺憾值（Regret）

假設對手的策略是固定的（unchanging）。然後對每手牌在遊戲樹中每個節點的每個可能行動運行上述期望值計算。然後我們選擇每個點的最高期望值決策，並從終端節點向後計算不同行動從第一個決策點的期望值。

好吧，我們知道了每手牌在每個節點的價值。我們如何改進策略？這就是“遺憾值”（regret）的概念發揮作用的地方。

最小化遺憾值是所有GTO算法的基礎。最著名的算法是CFR——反事實遺憾最小化（Counterfactual Regret Minimization）。反事實遺憾是我們對不玩某個策略的遺憾程度。例如，如果我們棄牌（fold）後發現跟注（call）是更好的策略，我們就“遺憾”沒有跟注。數學上，它測量採取某行動相較於我們在該決策點的整體策略的收益或損失。

Regret = Action EV – Strategy EV

例如，如果我們當前手牌的策略是棄牌、跟注和全下（shove）各1/3的時間，且每個行動的期望值為（棄牌 = 0bb，跟注 = 7bb，全下 = 5bb），則我們當前策略的期望值為：

(⅓ x 0) + (⅓ x 7 bb) + (⅓ x 5bb) = 4bb

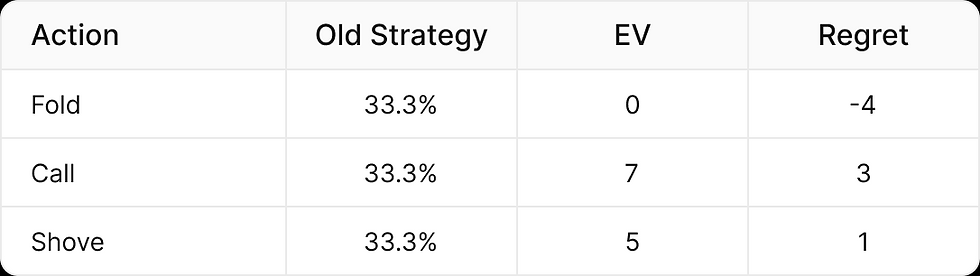
1. 棄牌有負遺憾值，意味著它比我們的平均策略損失更多。

2. 跟注和全下有正遺憾值，意味著它們優於我們的當前策略。

下一步是改變我們的策略以最小化遺憾值。

最明顯的方法是簡單地在每個決策點用每手牌選擇最高期望值的行動（即最大剝削策略，maximally exploitative strategy）。在上面的例子中，這意味著總是跟注。問題是對手可以改變他們的策略，這可能讓我們陷入循環。

例如，玩家A在河牌（river）低詐唬（under-bluffs），玩家B棄掉所有詐唬攔截牌（bluff-catchers），然後玩家A總是在河牌詐唬，然後玩家B跟注所有詐唬攔截牌，然後玩家A停止在河牌詐唬，無限重複。與其每次迭代完全切換到最佳回應，每個玩家可以朝該方向逐步調整策略。這解決了陷入循環的問題，並在策略對接近均衡時收斂更平滑。

我們可以使用CFR來更新我們的策略。回到之前的例子。任何具有負遺憾值的行動停止被使用。具有正遺憾值的行動使用以下公式：

New strategy = Action Regret / Sum of positive regrets

在我們的例子中，跟注 -> 3/(3+1) = 75%，全下 -> 1/(3+1) = 25%，而棄牌變為0%，因為它有負遺憾值。

當前策略期望值 = 4.0

新策略期望值 = 6.5

請注意，這只是一次迭代。隨著我們多次重複此過程，策略將接近一個雙方都無法改進的點，實現納什均衡。

精確度

解決方案的精確度通過其納什距離（Nash Distance）測量。我們從一個問題開始：

如果玩家A最大化剝削（maximally exploited）玩家B的當前策略，他們能贏多少？

這對電腦來說很容易計算，因為它已經知道遺憾值。玩家A當前策略的期望值與其最大剝削策略的期望值之間的差異代表其納什距離。這個數字越小，策略越不可剝削（unexploitable）且越精確。

我們取所有玩家的納什距離平均值來找到解決方案的精確度。

這些精確的納什距離測量僅在每次迭代枚舉整個策略時有效。大多數翻牌前求解器（preflop solvers）使用抽象化和抽樣方法，這使得這些計算不切實際且不準確。像HRC或Monker這樣的求解器通過測量每次迭代的策略/遺憾值變化來估計收斂。

GTO策略在納什距離低於底池的1%時開始收斂。超過這個閾值，策略極度混合（mixed）且往往不可靠。大多數職業玩家認為高於底池0.5%的納什距離是不可接受的。GTO Wizard根據解決方案類型解決到0.1%到0.3%的起始底池精確度。您的遊戲樹越複雜，區分相似下注大小所需的精確度越高。相似的大小導致相似的回報，因此具有許多下注大小的複雜遊戲樹需要更高的精確度來收斂。

凸收益空間（convex payoff space）

我們如何知道這種迭代方法有效？我們會不會陷入局部最大值？撲克一般可以描述為“雙線性鞍點問題”（bilinear saddle point problem）。收益空間（payoff space）看起來像這樣：

• x軸和y軸上的每個點代表一對策略。每對策略包含關於兩位玩家如何在每個場景、每個牌面運行（runout）中玩他們整個範圍（range）的信息。

• 高度（z軸）表示策略對的期望值，較高的點表示一個玩家的期望值優勢，較低的點表示另一個玩家的優勢。

大多數求解器使用一種稱為反事實遺憾最小化（Counterfactual Regret Minimization, CFR）的算法。該算法於2007年由阿爾伯塔大學的Martin Zinkevich在一篇論文中首次發表。該論文證明CFR算法不會陷入局部最大值，給予足夠的時間，將達到均衡。

這個鞍點的中心代表納什均衡（Nash Equilibrium）。圖表上的這一點（或多點）沒有曲率——意味著沒有玩家可以改變策略來改善回報。

進一步閱讀

• 我們強烈推薦閱讀這篇文章以了解更多關於撲克中CFR的內容。

• 這個網站提供了構建簡單CFR算法的絕佳教程和逐步說明。

• 關於在撲克中使用CFR的學術資源。

• Deep CFR – 應用神經網絡加速CFR計算。

• 通過“折扣”遺憾最小化（Discounted regret minimization）改進原始CFR算法。

結論

哇，這是大量信息！希望您現在對求解器的實際運作方式有更深入的理解。讓我們回顧主要要點：

• 從實際角度來看，主要結論是求解器是最大化期望值（EV-maximizing）的算法，利用我們提供的遊戲樹。要練習這些最大化期望值的策略，考慮嘗試GTO Wizard遊戲模式（Play Mode），通過真實遊戲來完善您的理解，使學習更具互動性和樂趣。

• 求解器算法生成最大剝削策略（max-exploit strategies）。讓這些算法相互對抗會產生不可剝削的均衡策略（unexploitable equilibrium strategies）。

• 計算一對策略的期望值對電腦來說是容易的部分。逐步調整策略並無數次迭代這個過程是困難的部分。

• 撲克太複雜，無法直接解決，因此我們使用限制下注大小（bet sizes）等抽象化技術（abstraction techniques）簡化遊戲空間。

• 求解器的精確度僅與您給予的抽象遊戲一樣。過多的複雜性無法解決，且人類難以學習。過多的簡單性導致求解器剝削該遊戲樹的局限性。